Mathematik mal ganz anders!
Die einen nennen die Mathematik eine Hilfswissenschaft, die anderen nennen sie ein mächtiges Werkzeug zur Beschreibung naturgesetzlicher Phänomene, wie dem Elektromagnetismus. In jedem Falle aber – und da sind sich alle einig – hilft uns die Mathematik, komplexe alltägliche Problemstellungen zu lösen. Dass es dabei nicht unbedingt auf die Lösung selbst, sondern vor allem auch auf den Lösungsweg ankommt, ist weniger eine Binsenweisheit vieler Mathematiklehrerinnen und -lehrer als vielmehr eine notwendige Prämisse zur Lösung solcher alltäglichen Problemstellungen. Warum? Schauen wir uns ein Beispiel an oder noch besser: drei Beispiele. Denn aus genau so vielen konnten sich unsere Schülerinnen und Schüler im Rahmen der jedes Jahr stattfindenden Modellierungstage der 10. Klassen am Helene-Lange-Gymnasium eines zur Bearbeitung aussuchen.
„An Aktualität hat es den Aufgaben nicht gefehlt, im Gegenteil: Selten waren sie aktueller.“
Das Spannende daran: Die Aufgaben sind so allgemein gehalten, dass die Problemlösung vor allem davon abhängt, welche Grundannahmen man getroffen hat – Modellierung eben. Das Besondere daran: An Aktualität hat es den Aufgaben nicht gefehlt, im Gegenteil: Selten waren sie aktueller. Das sorgte für reichlich Motivation! Im Konkreten lauteten die Aufgaben:
1) Steuerung einer Seilkamera: Entwickelt ein Verfahren zur Steuerung der Kamera.
2) Dein CO2-Fußabdruck: Erstelle einen CO2-Rechner, der für dich und deine Mitschülerinnen und Mitschüler passend ist.
3) Lüften im Klassenraum: Begründet die Anordnung, alle 20 Minuten zu lüften, mithilfe mathematischer Verfahren.
Die Herausforderung daran: die Offenheit! Wie gehe ich an diese Aufgaben heran? Welche Annahmen treffe ich? Gibt es überhaupt eine eindeutige Lösung und wenn ja, kann ich diese mit Hilfe einer Formel bestimmen?
Hier eine Lösung zur dritten Aufgabe, bei der zugrunde gelegt wird, dass eine Person ca. 250 ml CO2/Minute durch die Atmung ausstößt, der CO2-Gehalt in einem leeren Raum 400 ppm beträgt und man ab einem CO2-Gehalt von 1000 ppm lüften sollte.
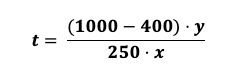
y: Rauminhalt in m³
x: Personenanzahl im Raum
Für einen durchschnittlichen Klassenraum mit einem Rauminhalt von ca. 200 m³ und einer Personenanzahl im Raum von 28 Personen (inkl. Lehrkraft) ergibt dies ein Lüftungsintervall von 17 Min. Das passt schon mal recht gut!
Wie ist es bei Ihnen zu Hause? Lüften Sie in ausreichenden Abständen? Finden Sie es heraus, indem Sie die entsprechenden Werte in die Formel einsetzen. Möglicherweise beruht die Formel Ihrer Meinung nach aber auch auf den falschen Annahmen. Dann ändern Sie sie ab und rechnen Sie erneut. Mathematik eben mal ganz anders!
Kenny Fritz, Fachleitung Mathematik










